CTC几种常见的解码方式

  1. greedy decode，每帧输出最大值，然后规整。
  2. 在ctc字符串上做beam search，输出的n个结果规整，并合并相同序列，然后再应用语言模型。(secondpass LM)
  3. 在规整字符串上做beam search, 可额外在应用语言模型。该算法叫Prefix Beam Search，可以在解码过程中直接应用LM。(firstpass LM)
  4. 使用fst静态解码。可引入语言模型和字典模型。

prefix beam search的笔记

本文为prefix beam search的笔记。

Grave最早提出的prefix search不好理解，现在也没有人用。可直接参考Awni Hannun提出的prefix beam search。

定义两个概念

  • ctc字符串:模型在每个时间点输出的字符组成的字符串。
  • 规整字符串:即ctc字符串去除连续重复和blank后的字符串。

prefix beam search基本思想:

  • 在每个时刻t，计算所有当前可能输出的规整字符串（即去除连续重复和blank的字符串）的概率。
  • 因为t时刻的规整字符串长度最长为t，最短为0(全都是blank，所以规整完是0)，所有t时刻所有可能的候选规整字符串个数是\(\sum_{0}^{t}{C^t}\)，其中C是字符词典大小。 该值随着t的增大而增大，穷举搜索空间太大。
  • 用beam search的方法，在每个时刻选取最好的N个路径，从而将每个时间点t上的搜索空间变为常数。

下图a表示一个规整字符串,表示其前缀，a表示其最后一个字符是a，箭头表示t+1时刻的字符串可能由哪些t时刻的字符串产生。

比如t+1时刻的*ab来自于两种情况：

  • t时刻输出规整字符串*a，t+1时刻输出字符b
  • t时刻输出规整字符串*ab，t+1时刻输出字符b

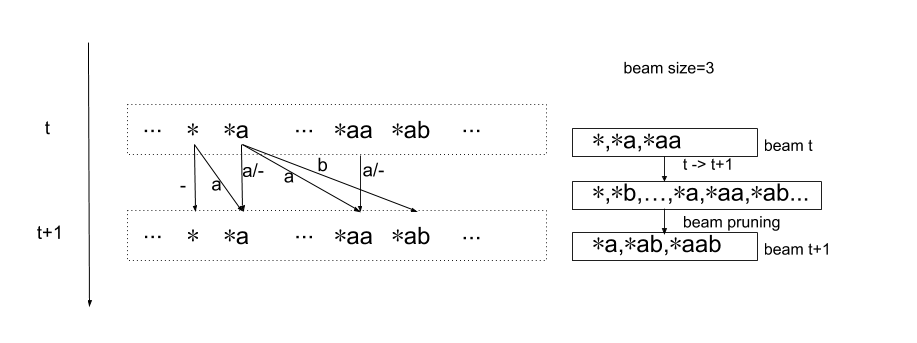
prefix_beam1

一个直接的想法是，对t时刻处在beam中的每个规整字符串，更新其对应的t+1时刻规整字符串的概率值。

但是这里并不能直接使用t时刻规整字符串的概率乘上t+1时刻输出字符概率得到t+1时刻规整字符串的概率。

我们看一个具体例子，假设第3时刻输出规整字符串a，第4时刻输出字符b。该规整字符串a的概率为-a-,-aa,aa-,aaa等不同的ctc字符串的概率和。

  • 如果是在aa-这个ctc字符串基础上，在t+1时刻再输出a,得到的ctc字符串为aa-a，其规整字符串为aa.
  • 如果是在aaa这个ctc字符串基础上，在t+1时刻再输出a,得到的ctc字符串为aaaa，其规整字符串为a.

可以看到两者使用同样的t+1的输出字符，却产生了不同的规整字符串。因此，需要区分对待blank和非blank结尾的ctc字符的规整概率:

  • \(p_b(L)\) 表示所有以blank结尾且规整后是L的各ctc字符串的概率之和
  • \(p_nb(L)\) 表示所有以非blank结尾且规整后是L的各ctc字符串的概率之和

比如，假设T=3，则 \(\begin{aligned} & p_b(a) = p(aa-) + p(-a-) + p(a--) \\ & p_{nb}(a) = p(aaa)+p(-aa) + p(--a) \\ \end{aligned}\)

这里只随便看其中一个，比如\(*a\), 其t+1时刻可以产生规整字符串有四种情况。

  • 当t+1输出是blank时，产生规整字符串*a
  • 当t+1输出是a时，可以产生规整字符串*a
  • 当t+1输出是a时，也可产生规整字符串*aa
  • 当t+1输出是b时(或其他不等于a和blank的字符)，产生规整字符串*ab

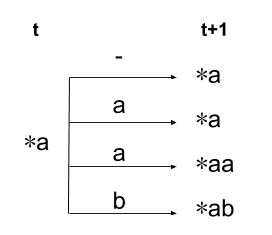
prefix_beam2

四种情况对应的需要更新的统计量的公式如下

\[\begin{aligned} & p_{b}^{t+1}(*a)\! & \Leftarrow & \;[ p_{b}^{t}(*a) + p_{nb}^{t}(*a) ] p_{ctc}^{t+1}(-) \\ & p_{nb}^{t+1}(*a)\! & \Leftarrow & \;p_{nb}^{t}(*a)p_{ctc}^{t+1}(a) \\ & p_{nb}^{t+1}(*aa)\! & \Leftarrow & \;p_{b}^{t}(*a)p_{ctc}^{t+1}(a) \\ & p_{nb}^{t+1}(*ab)\! & \Leftarrow & \;[p_{b}^{t}(*a) + p_{nb}^{t}(*a)]p_{ctc}^{t+1}(b) \\ \end{aligned}\]
  • \(\Leftarrow\) 不是赋值，而是C语言中的+=操作。
  • 注意， \(p_{nb}^{t+1}(*ab)\)的值不仅来源于t时刻beam里的*a路径， 在对t时刻beam里的*b路径进行更新t+1的路径时，也会贡献概率。
\[\begin{aligned} & p_{nb}^{t+1}(*b)\! & \Leftarrow & \;p_{nb}^{t}(*b)p_{ctc}^{t+1}(b) \\ \end{aligned}\]

说明

ctc字符串上的beam search和规整字符串上的beam search的区别:

  1. 同样的beam size下ctc字符串上的beam search，其丢掉的ctc路径比在规整字符串上做beam search的更多，所以最终的结果就更差一些。

参考Awni在Distill上的文章中的图片

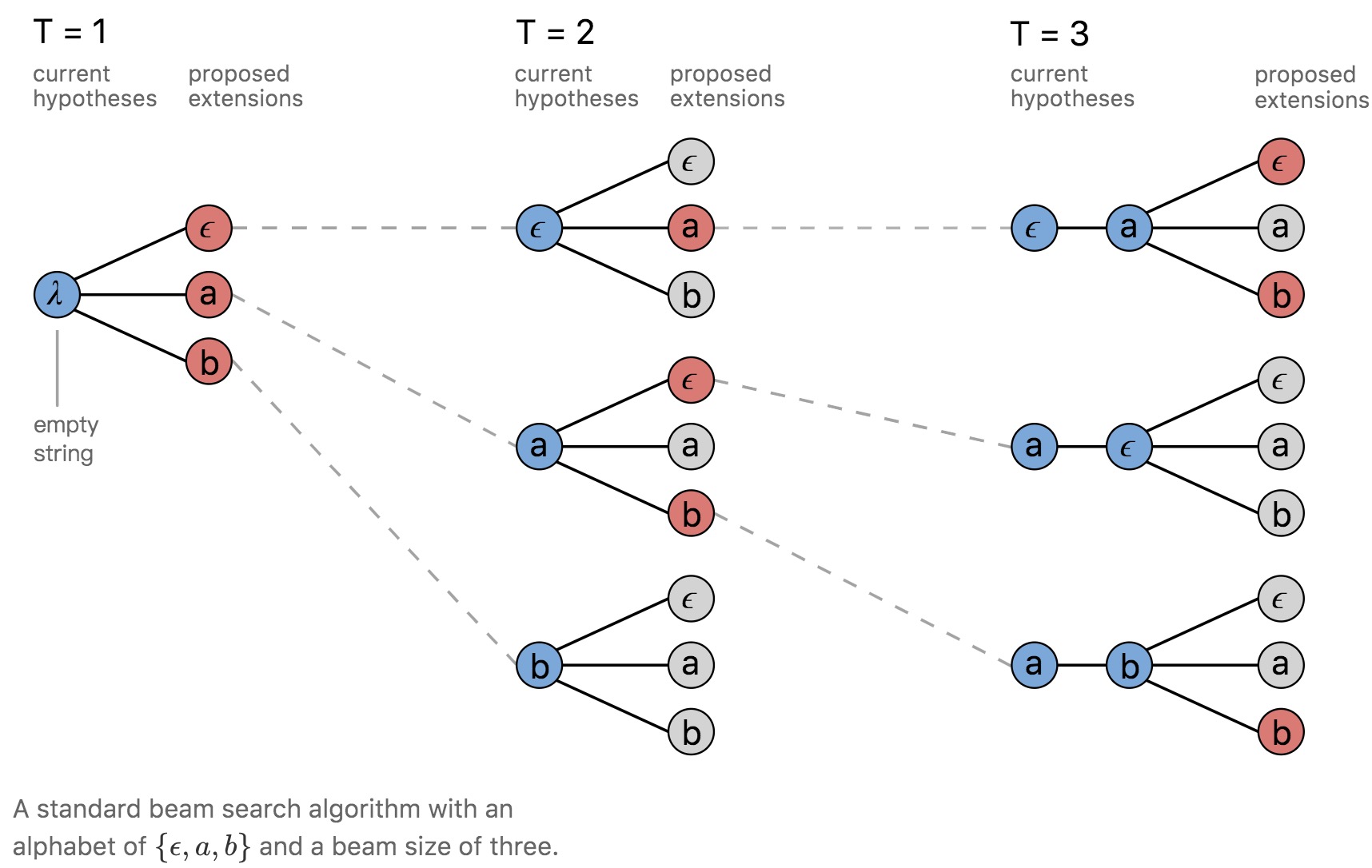
直接做beam search，可以看到beam size=3时，每个时刻只有三个路径v ctc_beamsearch

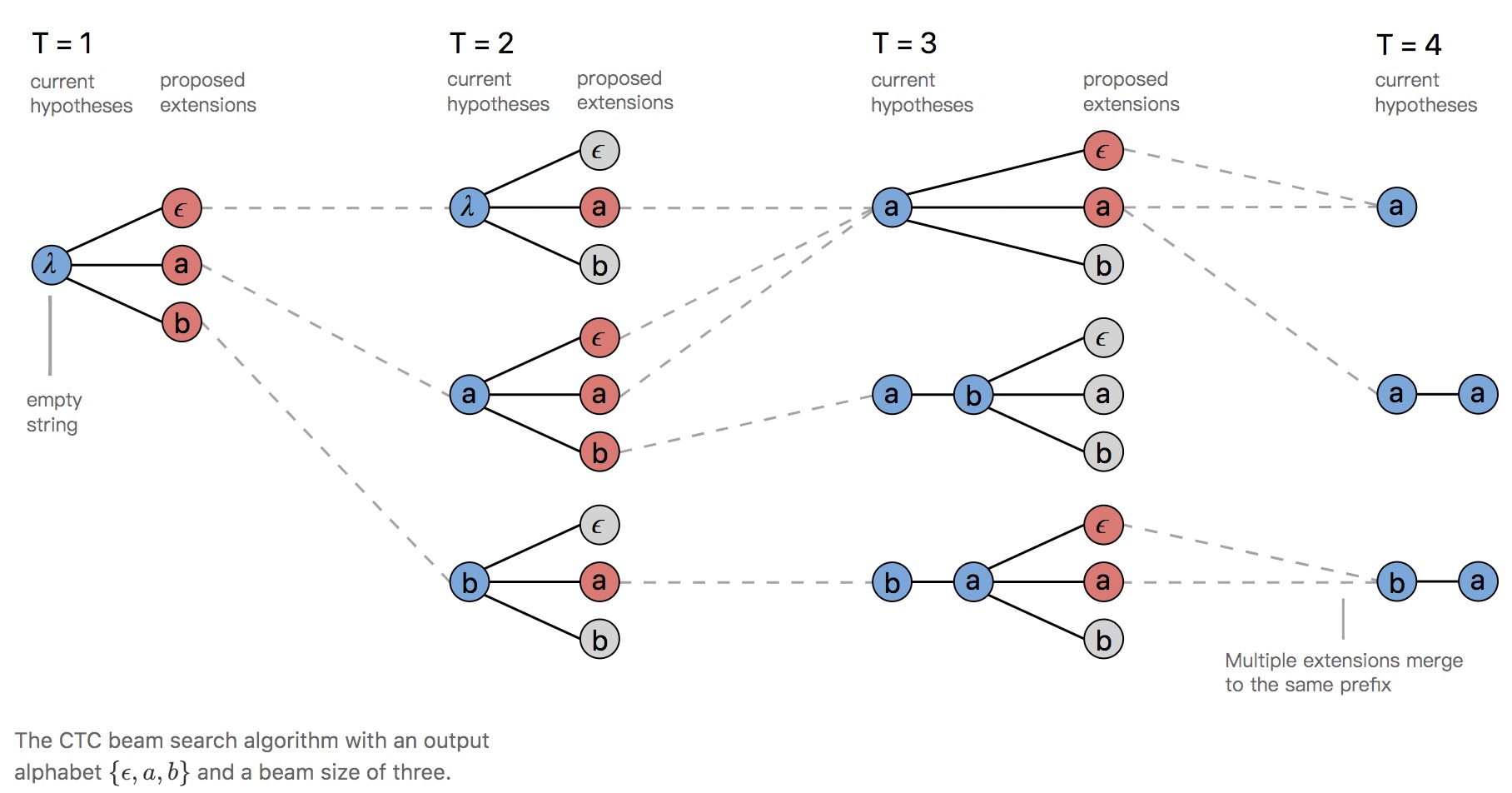
在规整字符串上做beam search，可以看到beam size=3时，每个时刻可以保留更多路径 prefix_beamsearch

Prefix beam search仍然会丢失一些ctc序列的概率，比如上例中，字符串ba里没有包含blank blank blank blank b a这条CTC序列。

  1. 在规整字符串上做beam search允许在fisrt pass引入LM得分，因为解码过程中就知道规整后的形式和space的位置，在ctc字符串上做beam search则不行。

Hannun论文《First-Pass Large Vocabulary Continuous Speech Recognition using Bi-Directional Recurrent DNNs 》中给出的算法。 prefix_beam_algo 注意两点:

  • 可以在first pass里引入word LM的得分，只要在输出space的时候加入语言模型的得分。
  • if $l^{+}$ not in $A_{prev}$ 的作用.当t时刻的beam里只有a而没有ab时，在t+1时刻计算ab，只使用了t时刻a的扩展，会丢失来自t时刻*ab的得分。

Hannun给出的一个python实现。

"""
Author: Awni Hannun

This is an example CTC decoder written in Python. The code is
intended to be a simple example and is not designed to be
especially efficient.

The algorithm is a prefix beam search for a model trained
with the CTC loss function.

For more details checkout either of these references:
  https://distill.pub/2017/ctc/#inference
  https://arxiv.org/abs/1408.2873

"""

import numpy as np
import math
import collections

NEG_INF = -float("inf")

def decode(probs, beam_size=10, blank=0):
    """
    Performs inference for the given output probabilities.

    Arguments:
      probs: The output probabilities (e.g. log post-softmax) for each
        time step. Should be an array of shape (time x output dim).
      beam_size (int): Size of the beam to use during inference.
      blank (int): Index of the CTC blank label.

    Returns the output label sequence and the corresponding negative
    log-likelihood estimated by the decoder.
    """
    T, S = probs.shape

    # Elements in the beam are (prefix, (p_blank, p_no_blank))
    # Initialize the beam with the empty sequence, a probability of
    # 1 for ending in blank and zero for ending in non-blank
    # (in log space).
    beam = [(tuple(), (0.0, NEG_INF))]

    for t in range(T): # Loop over time

        # A default dictionary to store the next step candidates.
        next_beam = make_new_beam()

        for s in range(S): # Loop over vocab
            p = probs[t, s]

            # The variables p_b and p_nb are respectively the
            # probabilities for the prefix given that it ends in a
            # blank and does not end in a blank at this time step.
            for prefix, (p_b, p_nb) in beam: # Loop over beam

                # If we propose a blank the prefix doesn't change.
                # Only the probability of ending in blank gets updated.
                if s == blank:
                  n_p_b, n_p_nb = next_beam[prefix]
                  n_p_b = logsumexp(n_p_b, p_b + p, p_nb + p)
                  next_beam[prefix] = (n_p_b, n_p_nb)
                  continue

                # Extend the prefix by the new character s and add it to
                # the beam. Only the probability of not ending in blank
                # gets updated.
                end_t = prefix[-1] if prefix else None
                n_prefix = prefix + (s,)
                n_p_b, n_p_nb = next_beam[n_prefix]
                if s != end_t:
                  n_p_nb = logsumexp(n_p_nb, p_b + p, p_nb + p)
                else:
                  # We don't include the previous probability of not ending
                  # in blank (p_nb) if s is repeated at the end. The CTC
                  # algorithm merges characters not separated by a blank.
                  n_p_nb = logsumexp(n_p_nb, p_b + p)

                # *NB* this would be a good place to include an LM score.
                next_beam[n_prefix] = (n_p_b, n_p_nb)

                # If s is repeated at the end we also update the unchanged
                # prefix. This is the merging case.
                if s == end_t:
                  n_p_b, n_p_nb = next_beam[prefix]
                  n_p_nb = logsumexp(n_p_nb, p_nb + p)
                  next_beam[prefix] = (n_p_b, n_p_nb)

        # Sort and trim the beam before moving on to the
        # next time-step.
        beam = sorted(next_beam.items(),
                key=lambda x : logsumexp(*x[1]),
                reverse=True)
        beam = beam[:beam_size]

    best = beam[0]
    return best[0], -logsumexp(*best[1])

参考资料：

  1. https://distill.pub/2017/ctc/
  2. https://arxiv.org/abs/1408.2873
  3. https://towardsdatascience.com/beam-search-decoding-in-ctc-trained-neural-networks-5a889a3d85a7