Relative Positional Embedding
本文讲解基于transformer/conformer的语音识别Wenet中的Relative Positional Embed的实现
Relative Positional Embedding
Transformer XL中提出了Relative Positional Embedding方法,在ASR conformer论文中,也提到
We employ multi-headed self-attention (MHSA) while integrating an important technique from Transformer-XL [20],the relative sinusoidal positional encoding scheme. The relative po- sitional encoding allows the self-attention module to generalize better on different input length and the resulting encoder is more robust to the variance of the utterance length.
原始的带positional embedding的 attention score计算方法
i位置的encoding embedding为\(\mathbf{E}_{x_{i}}\),positional embedding信息\(\mathbf{U}_{k}\), i和j位置的attention score计算如下:
\[\begin{equation} \left(\mathbf{E}_{x_{i}}^{\top}+\mathbf{U}_{i}^{\top}\right) \mathbf{W}_{q}^{\top} \mathbf{W}_{k}\left(\mathbf{E}_{x_{j}}+\mathbf{U}_{j}\right) \end{equation}\]展开得到
\[\begin{equation} \begin{aligned} \mathbf{A}_{i, j}^{\mathrm{abs}} &=\underbrace{\mathbf{E}_{x_{i}}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k} \mathbf{E}_{x_{j}}}_{(a)}+\underbrace{\mathbf{E}_{x_{i}}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k} \mathbf{U}_{j}}_{(b)} \\ &+\underbrace{\mathbf{U}_{i}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k} \mathbf{E}_{x_{j}}}_{(c)}+\underbrace{\mathbf{U}_{i}^{\top} \mathbf{W}_{q}^{\top} \mathbf{W}_{k} \mathbf{U}_{j}}_{(d)} \end{aligned} \end{equation}\]去除\(\mathbf{W}_{q}\)和\(\mathbf{W}_{k}\)简化形式:
\[\begin{equation} \mathbf{A}_{i, j}^{\mathrm{abs}}=\underbrace{\mathbf{E}_{x_{i}}^{\top} \mathbf{E}_{x_{j}}}_{(a)}+\underbrace{\mathbf{E}_{x_{i}}^{\top} \mathbf{U}_{j}}_{(b)}+\underbrace{\mathbf{U}_{i}^{\top} \mathbf{E}_{x_{j}}}_{(c)}+\underbrace{\mathbf{U}_{i}^{\top} \mathbf{U}_{j}}_{(d)} \end{equation}\]Relative Positional Embedding
相对位置这个概念,只有做attention时才存在, 使用\(R_{i-j}\)表示第i个位置的query和第j个位置的key做attention时用的相对距离信息:
- 第3个位置的query和第2个位置的key做attention,使用R1.
- 第4个位置的query和第3个位置的key做attention,使用R1.
- 第4个位置的query和第2个位置的key做attention,使用R2.
在引入两个跟位置无关的可学习的向量参数u和v,将上述的带位置信息的attention score计算改写为:
\[\begin{equation} \mathbf{A}_{i, j}^{\mathrm{rel}}=\underbrace{\mathbf{E}_{x_{i}}^{\top} \mathbf{E}_{x_{j}}}_{(a)}+\underbrace{\mathbf{E}_{x_{i}}^{\top} \mathbf{R}_{i-j}}_{(b)}+\underbrace{\mathbf{u}^{\top} \mathbf{E}_{x_{j}}}_{(c)}+\underbrace{\mathbf{v}^{\top} \mathbf{R}_{i-j}}_{(d)} \end{equation}\]合并ac项,bd项:
\[\begin{equation} \mathbf{A}_{i, j}^{\mathrm{rel}}=\underbrace{\left(\mathbf{E}_{x_{i}}^{\top}+\mathbf{u}^{\top}\right) \mathbf{E}_{x_{j}}}_{(a c)}+\underbrace{\left(\mathbf{E}_{x_{i}}^{\top}+\mathbf{v}^{\top}\right) \mathbf{R}_{i-j}}_{(b d)} \end{equation}\]这个score matrix可以写成下面两项之和
\[\begin{equation} \mathbf{A}^{\mathrm{rel}}=\mathbf{A}_{a c}+\mathbf{A}_{b d} \end{equation}\]ac项容易计算,这里只关注bd项, 为了表示方便,用\(R_{j-i}\)代替\(R_{i-j}\), 同时令 \(\mathbf{q}_{i} = \mathbf{E}_{x_{i}} + \mathbf{v}\)
\[\begin{equation} \mathbf{A}_{b d}=\left[\begin{array}{cccc} q_{0}^{\top} \mathbf{R}_{0} & q_{0}^{\top} \mathbf{R}_{1} & \cdots & q_{0}^{\top} \mathbf{R}_{L-1} \\ q_{1}^{\top} \mathbf{R}_{-1} & q_{1}^{\top} \mathbf{R}_{0} & \cdots & q_{1}^{\top} \mathbf{R}_{L-2} \\ \vdots & \vdots & \ddots & \vdots \\ q_{L-1}^{\top} \mathbf{R}_{-(L-1)} & q_{L-1}^{\top} \mathbf{R}_{-(L-2)} & \cdots & q_{L-1}^{\top} \mathbf{R}_{0} \end{array}\right] \end{equation}\]一种计算\(\mathbf{A}_{bd}\) 的方法是对于矩阵中的每一项分别计算。但是无法利用到GPU对大矩阵相乘加速的优点。有没有办法把矩阵\(\mathbf{A}_{bd}\) 的计算变为矩阵乘法呢?可以使用下面方法
令
\[\begin{equation} \mathbf{R}=\left[\begin{array}{llllll} \mathbf{R}_{-(L-1)} & \mathbf{R}_{-(L-2)} & \mathbf{R}_{0} & \cdots & \mathbf{R}_{L-2} & \mathbf{R}_{L-1} \end{array}\right] \end{equation}\] \[\begin{equation} \mathbf{q}=\left[\begin{array}{c} \mathbf{q}_{0}^{\top} \\ \mathbf{q}_{1}^{\top} \\ \vdots \\ \mathbf{q}_{L-1}^{\top} \\ \mathbf{q}_{L}^{\top} \end{array}\right] \end{equation}\]两个矩阵相乘,得
\[\begin{equation} \mathbf{q} \mathbf{R}=\left[\begin{array}{ccccccc} q_{0}^{\top} \mathbf{R}_{-(L-1)} & q_{0}^{\top} \mathbf{R}_{-(L-2)} & \cdots & q_{0}^{\top} \mathbf{R}_{0} & \cdots & q_{0}^{\top} \mathbf{R}_{L-2} & q_{0}^{\top} \mathbf{R}_{L-1} \\ q_{1}^{\top} \mathbf{R}_{-(L-1)} & q_{1}^{\top} \mathbf{R}_{-(L-2)} & \cdots & q_{1}^{\top} \mathbf{R}_{0} & \cdots & q_{1}^{\top} \mathbf{R}_{L-2} & q_{1}^{\top} \mathbf{R}_{L-1} \\ \vdots & \vdots & \ddots & \vdots & \ddots & \vdots & \vdots \\ q_{L-1}^{\top} \mathbf{R}_{-(L-1)} & q_{L-1}^{\top} \mathbf{R}_{-(L-2)} & \cdots & q_{L-1}^{\top} \mathbf{R}_{0} & \cdots & q_{L-1}^{\top} \mathbf{R}_{L-2} & q_{L-1}^{\top} \mathbf{R}_{L-1} \end{array}\right] \end{equation}\]对该矩阵,将第i行左移L-i个位置,并且取前L列即得到\(\mathbf{A}_{bd}\)
\[\begin{equation} \mathbf{A}_{b d}=\left[\begin{array}{cccc} q_{0}^{\top} \mathbf{R}_{0} & q_{0}^{\top} \mathbf{R}_{1} & \cdots & q_{0}^{\top} \mathbf{R}_{L-1} \\ q_{1}^{\top} \mathbf{R}_{-1} & q_{1}^{\top} \mathbf{R}_{0} & \cdots & q_{1}^{\top} \mathbf{R}_{L-2} \\ \vdots & \vdots & \ddots & \vdots \\ q_{L-1}^{\top} \mathbf{R}_{-(L-1)} & q_{L-1}^{\top} \mathbf{R}_{-(L-2)} & \cdots & q_{L-1}^{\top} \mathbf{R}_{0} \end{array}\right] \end{equation}\]以上是一个长为L的序列中进行fully-attention的计算方式,对于的非流式E2E ASR系统,encoder部分使用上述fully-attention方法即可,对于流式的系统,一般可采用chunk-based,即当前chunk内的帧要和前面的帧以及本chunk内的帧做attention。在transformer-XL中,也是类似的方法: 当前长度为\(L\)的segment和他前面长度为\(M\)的memory以及自己segment内部的各个点做attention。
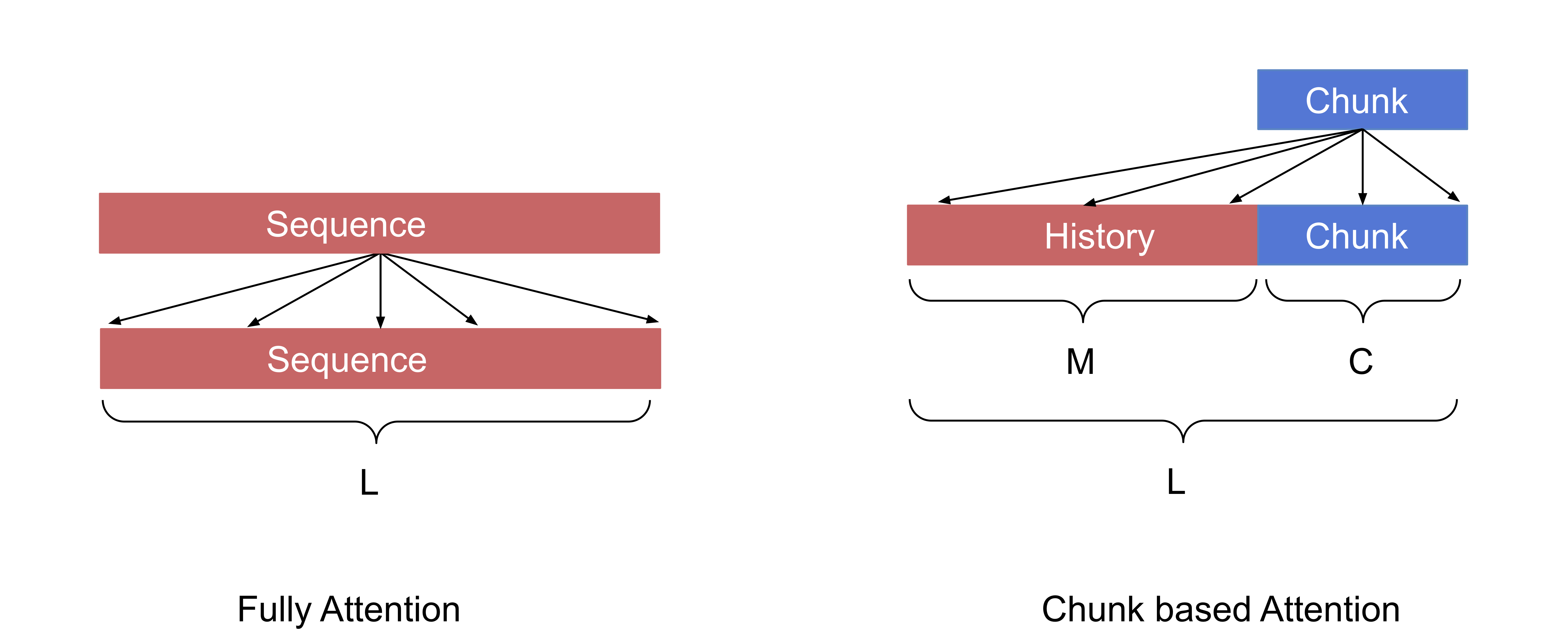
下面是chunk based attention下的计算方法,fully-attention只是chunk based attention的一个特例,即chunk size=整个序列长度的情况。
假设当前chunk的大小为\(C\),之前帧数为\(M\),则对于每个chunk,query的个数为\(C\)个,key/value的个数为\(M+C\)个。
只需将\(\mathbf{q} \mathbf{R}\)第\(i\)行左移\(C-i\)个位置即可得到对应的score matrix 令 \(L=M+C\) ,则当前chunk的score matrix计算方式如下:
\[\begin{equation} \mathbf{A}_{b d}=\left[\begin{array}{cccc} q_{0}^{\top} \mathbf{R}_{-(L-C)} & q_{0}^{\top} \mathbf{R}_{L-C+1} & \cdots & q_{0}^{\top} \mathbf{R}_{C-1} \\ q_{1}^{\top} \mathbf{R}_{-(L-C+1)} & q_{1}^{\top} \mathbf{R}_{L-C} & \cdots & q_{1}^{\top} \mathbf{R}_{C-2} \\ \vdots & \vdots & \ddots & \vdots \\ q_{C-1}^{\top} \mathbf{R}_{-(L-1)} & q_{C-1}^{\top} \mathbf{R}_{-(L-2)} & \cdots & q_{C-1}^{\top} \mathbf{R}_{0} \end{array}\right] \end{equation}\]代码实现
产生Relative Positional Embedding
生成一个[-L,L]的Relative Positional Embedding的方法:
class RelPositionalEncoding():
def __init__(self,
d_model: int,
dropout_rate: float,
max_len: int = 5000):
super().__init__()
self.d_model = d_model
self.max_len = max_len
self.pe = torch.zeros(self.max_len, self.d_model)
position = torch.arange(0, self.max_len,
dtype=torch.float32).unsqueeze(1)
div_term = torch.exp(
torch.arange(0, self.d_model, 2, dtype=torch.float32) *
-(math.log(10000.0) / self.d_model))
self.pe[:, 0::2] = torch.sin(position * div_term)
self.pe[:, 1::2] = torch.cos(position * div_term)
def position_encoding(self, size: int) -> torch.Tensor:
assert size < int(self.max_len/2)
mid_pos = int(self.max_len / 2)
pos_emb = self.pe[mid_pos - size + 1:mid_pos + size]
return pos_emb
Attention计算
利用上面生成的 \(2*L-1\) 长度的Relative Positional Embedding和Query Embeddings做矩阵乘法, 计算方式和Multi-Head Attention类似
def forward(self, query: torch.Tensor, key: torch.Tensor,
value: torch.Tensor, pos_emb: torch.Tensor,
mask: Optional[torch.Tensor]):
"""Compute 'Scaled Dot Product Attention' with rel. positional encoding.
Args:
query (torch.Tensor): Query tensor (#batch, time1, size).
key (torch.Tensor): Key tensor (#batch, time2, size).
value (torch.Tensor): Value tensor (#batch, time2, size).
pos_emb (torch.Tensor): Positional embedding tensor
(2*time2-1, size).
mask (torch.Tensor): Mask tensor (#batch, time1, time2).
Returns:
torch.Tensor: Output tensor (#batch, time1, d_model).
"""
q, k, v = self.forward_qkv(query, key, value)
q = q.transpose(1, 2) # (batch, time1, head, d_k)
p = self.linear_pos(pos_emb).view(-1, self.h, self.d_k) # (2*time2-1, head, d_k)
p = p.transpose(0, 1) # (head, 2*time2-1, d_k)
# (batch, head, time1, d_k)
q_with_bias_u = (q + self.pos_bias_u).transpose(1, 2)
# (batch, head, time1, d_k)
q_with_bias_v = (q + self.pos_bias_v).transpose(1, 2)
# compute attention score
# first compute matrix a and matrix c
# as described in https://arxiv.org/abs/1901.02860 Section 3.3
# (batch, head, time1, time2)
matrix_ac = torch.matmul(q_with_bias_u, k.transpose(-2, -1))
# compute matrix b and matrix d
# (batch, head, time1, 2*time2 -1)
matrix_bd = torch.matmul(q_with_bias_v, p.transpose(-2, -1))
# Remove rel_shift since it is useless in speech recognition,
# and it requires special attention for streaming.
matrix_bd = self.rel_shift(matrix_bd)
matrix_bd = matrix_bd[:, :, :, :matrix_ac.size(3)]
scores = (matrix_ac + matrix_bd) / math.sqrt(
self.d_k) # (batch, head, time1, time2)
return self.forward_attention(v, scores, mask)
其中matrix_bd的计算:
p = self.linear_pos(pos_emb).view(-1, self.h, self.d_k) # (2*time2-1, head, d_k)
p = p.transpose(0, 1) # (head, 2*time2-1, d_k)
matrix_bd = torch.matmul(q_with_bias_v, p.transpose(-2, -1))
matrix_bd = self.rel_shift(matrix_bd)
matrix_bd = matrix_bd[:, :, :, :matrix_ac.size(3)]
Attention Score矩阵左移操作
rel_shift会对一个矩阵进行左移操作。
def rel_shift(self, x):
"""Compute relative positinal encoding.
Args:
x (torch.Tensor): Input tensor (batch, head, time1, time2)
(batch, time, size).
zero_triu (bool): If true, return the lower triangular part of
the matrix.
Returns:
torch.Tensor: Output tensor.
"""
zero_pad = torch.zeros((x.size(0), x.size(1), x.size(2), 1),
device=x.device,
dtype=x.dtype)
x_padded = torch.cat([zero_pad, x], dim=-1)
x_padded = x_padded.view(x.size(0),
x.size(1),
x.size(3) + 1, x.size(2))
x = x_padded[:, :, 1:].view_as(x)
return x
下面以C=3,L=4举例,
对于一个C x (2L-1)的矩阵,总共用C*(2L-1)个元素,
tensor([[[[ 1., 2., 3., 4., 5., 6., 7.],
[ 8., 9., 10., 11., 12., 13., 14.],
[ 15., 16., 17., 18., 19., 20., 21.]]]])
每一行开头增加一个0,
tensor([[[[ 0., 1., 2., 3., 4., 5., 6., 7.],
[ 0., 8., 9., 10., 11., 12., 13., 14.],
[ 0., 15., 16., 17., 18., 19., 20., 21.]]]])
变为C*(2L-1)+C个元素,然后将行列展开成一行,
tensor([ 0., 1., 2., 3., 4., 5., 6., 7., 0., 8., 9., 10., 11., 12.,
13., 14., 0., 15., 16., 17., 18., 19., 20., 21.])
去除开头的C个元素,
tensor([ 3., 4., 5., 6., 7., 0., 8., 9., 10., 11., 12., 13., 14., 0.,
15., 16., 17., 18., 19., 20., 21.])
再排列成C x (2L-1)的矩阵。
tensor([[[[ 3., 4., 5., 6., 7., 0., 8.],
[ 9., 10., 11., 12., 13., 14., 0.],
[15., 16., 17., 18., 19., 20., 21.]]]])
取前L列
tensor([[[[ 3., 4., 5.],
[ 9., 10., 11.],
[15., 16., 17.]]]])